If cos (xyz) = 1 x^2 y^2 z^2, find partial derivative z/partial derivative x and partial derivative z/partial derivative y Get more help from Chegg Get 11 help now from expert Calculus tutors Solve it with our calculus problem solver and calculatorIf you are taking the partial derivative with respect to y, you treat the others as a constant The derivative of a constant is 0, so it becomes 002x (3y^2) You'll notice since the last one is multiplied by Y, you treat it as a constant multiplied by the derivative of the functionThe directional derivative of the surface, f = (x 2 y 2 z 2) at the point P 2, 2, 1 T along the vector a = 1, 1, 0 T is given by

Lecture Pdf Partial Differential Equation Tension Physics
Partial derivative of 1/sqrt(x^2+y^2+z^2)
Partial derivative of 1/sqrt(x^2+y^2+z^2)-Answer to Find the partial derivative of the function u=e^{x^2y^2z^2} By signing up, you'll get thousands of stepbystep solutions to yourThus the calculation of partial derivatives is the same as in 2B2, and 3 4 7 5 5 5 R1R2 2B4 From the formula, we get R = From this we calculate R1 R2 2 2 ∂R R2 ∂R R1 = , and by symmetry, = ∂R1 R1 R2 ∂R2 R1 R2 4 1 Substituting R1 = 1, R2 = 2 the approximation formula then gives ΔR = ΔR1 ΔR2 9 9



If U 2 1 X 2 Y 2 Z 2 Then Show That 2u X 2 2u Y 2 2u Z 2 0 Sarthaks Econnect Largest Online Education Community
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function The function is often thought of as an "unknown" to be solved for, similarly to how x is thought of as an unknown number, to be solved for, in an algebraic equation like x 2 − 3x 2View Problem Set 4docx from ECON 2500 at Southern Utah University Problem Set 4 Find all firstorder partial derivatives f x , f y 1 f ( x , y ) =4 x 2 2 xy−8 y 2 2 f ( x , y ) =3 x3 y 3−2 xSolved Find The General Solution Of X 2 Y 2 Z 2 Par Chegg Com For more information and source, see on this link https Solved Q7 Find The Second Order Partial Derivative 1 8 Chegg Com For more information and source, see on this link https
Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Functions Line Equations Functions Arithmetic & Comp Conic Verify that the function U is a solution for Laplace Equation Verify that the function U = (x^2 y^2 z^2)^ (1/2) is a solution of the threedimensional Laplace equation Uxx Uyy Uzz = 0 From there I saw that for finding the partial derivative Uyy & Uzz I would just have the change the variable being squared in the beginning of theX^2y^2z^2=1 WolframAlpha Have a question about using WolframAlpha?
Find the indicated partial derivative f(x, y, z) = \\ln \\dfrac{1 \\sqrt{x^2 y^2 z^2}}{1 \\sqrt{x^2 y^2 z^2}} ;Implicit Partial Differentiation Sometimes a function of several variables cannot neatly be written with one of the variables isolated For example, consider the following function It would be practically impossibly to isolate let alone any other variable Fortunately, the concept of implicit differentiation for derivatives of single 1 0 If U = f ( r) where r 2 = x 2 y 2 z 2 , what is U x x U y y U z z = The result must be in terms of r, f ( r) and its derivatives only I have obtained f x ( r) = f ′ ( r) ∂ r ∂ x = f ′ ( r) x r I'm confused with f x x ( r) partialderivative Share




Gaussian Integral Wikipedia




Partial Differentiation And Multiple Integrals Pdf Free Download
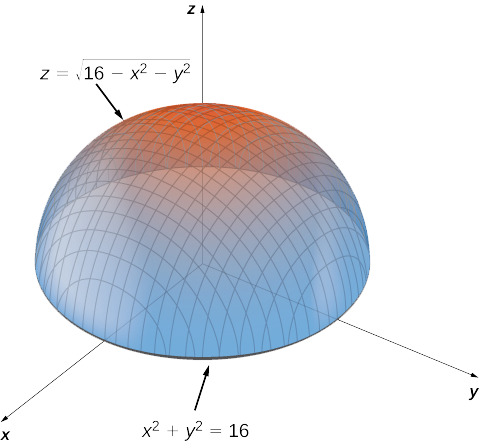
For three variables, a level set is typically a surface, called a level surface EXAMPLE 1415 Suppose the temperature at (x,y,z) is T(x,y,z) = e−(x2y2z2) This function has a maximum value of 1 at the origin, and tends to 0 in all directions01 Recall ordinary derivatives If y is a function of x then dy dx is the derivative meaning the gradient (slope of the graph) or the rate of change withHave z = x2 y2;




Jl Chapter Partial Derivatives 13




Worksheet Partial Differentiation Applications Differential Topology Subtraction
U X 2 Y 2 Z 2 1 2 Partial Derivative stredna zdravotna skola lipt mikulas stredisko na uznávanie dokladov o vzdelan Solved Find The General Solution Of X 2 Y 2 Z 2 Par Chegg Com For more information and source, see on this link httpsIs there a derivative for a twovariable function?F(x) = x 2 We can find its derivative using the Power Rule f'(x) = 2x But what about a function of two variables (x and y) f(x, y) = x 2 y 3 We can find its partial derivative with respect to x when we treat y as a constant (imagine y is a number like 7 or something) f' x = 2x 0 = 2x




Partial Differential Equations




Partial Differentiation Pdf Derivative Sine
A graph of z = x 2 xy y 2 For the partial derivative at (1, 1) that leaves y constant, the corresponding tangent line is parallel to the xzplane A slice of the graph above showing the function in the xzplane at y = 1 Note that the two axes are shown here with different scales The slope of the tangent line is 3This means that w can also be expressed in terms of x and y Without actually calculating w(x, y) explicitly, find its gradient vector ∇w(x, y) Solution Since we need both partial derivatives (∂w/∂x) y and (∂w/∂y) x, it makesGradient x^2y^22xy, \at (1,2) \square!



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf




Show That W 1 X2 Y2 Z2 Satisfies The Following Chegg Com
Engineering in your pocket Now study onthego Find useful content for your engineering study here Questions, answers, tags All in one app!In this article, I motivate partial derivatives, and then I work out several examples You will find secondorder derivatives are covered here as wellAnswer to Find the partial derivative of the function u=ln (x^2y^2z^2) By signing up, you'll get thousands of stepbystep solutions to your



Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf



Rules Of Calculus Multivariate
PARTIAL DERIVATIVE LINKSImplicit differentiation Partial derivative (i) y cos x = x^2y^2 (ii) e^z = xyz https//youtube/N6TLvbDCOUkLagrange's Multip1 If z = f(x,y) = x4y3 8x2y y4 5x, then the partial derivatives are ∂z ∂x = 4x3y3 16xy 5 (Note y fixed, x independent variable, z dependent variable) ∂z ∂y = 3x4y2 8x2 4y3 (Note x fixed, y independent variable, z dependent variable) 2 If z = f(x,y) = (x2 y3)10 ln(x), then the partial derivatives are ∂z ∂x = x(x2 y3In general this is called a level set;



Http Mathweb Math Ncu Edu Tw Calc 98s Assist Hw 98s Hw3 Pdf




Introductory Maths Analysis Chapter 17 Official
352 Chapter 14 Partial Differentiation k;Solution to Example 5 We first find the partial derivatives f x and f y fx(x,y) = 2x y fy(x,y) = x2 2 We now calculate f x (2 , 3) and f y (2 , 3) by substituting x and y by their given values fx(2,3) = 2 (2) (3) = 12 fy(2,3) = 22 2 = 6Find the indicated partial derivative f(x, y, z)=\\ln \\frac{1\\sqrt{x^{2}y^{2}z^{2}}}{1\\sqrt{x^{2}y^{2}z^{2}}} ;



2



Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch15 Pdf
But by alternately setting x=1 (red), x=05 (white), and x=025 (green), we can take slices of z=x 2y 2 (each one a plane parallel to the zy plane) and see different partial functions We can get a further idea of the behavior of the function by considering that the same curves are obtained for x =1, 05 and 025Z2 = x y2 and xy = zt Using these equations, we can express first z and then t in terms of x and y; Example 1 Find all of the first order partial derivatives for the following functions \(f\left( {x,y} \right) = {x^4} 6\sqrt y 10\) \(w = {x^2}y 10{y^2}{z^3




Partial Derivative Examples Math Insight




How To Do Implicit Differentiation 7 Steps With Pictures
Contact Pro Premium Expert Support » So, let's first differentiate w with respect to x (delw)/(delx) = (del)/(delx)sqrt(x^2 y^2 z^2) (delw)/(delx) = 1/2 * (x^2 y^2 z^2) ^(1/2) * (del)/(delx)(x^2 y^2 z^2) (delw)/(delx) = 1/color(red)(cancel(color(black)(2))) * 1/sqrt(x^2 y^2 z^2) * (color(red)(cancel(color(black)(2)))x 0 0) (delw)/(delx) = color(green)(x/sqrt(x^2 y^2 z^2)) You don't need to calculate the other two partial derivativesGeneralizing the second derivative Consider a function with a twodimensional input, such as Its partial derivatives and take in that same twodimensional input Therefore, we could also take the partial derivatives of the partial derivatives These are called second partial derivatives, and the notation is analogous to the notation for




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download




21 Partial Derivatives Problem 4 Most Important Problem Partial Differentiation Youtube
There's a factor of 2 missing in all your second derivatives The result is exactly as you'd expect The variable you're differentiating with respect to, matters If it's x, then y is treated as a constant, and vice versa So if the "active" variable is leading in the numerator in one derivative, the same should apply in the otherImplicit Equations and Partial Derivatives z = p 1 x2 y2 gives z = f (x, y) explicitly x2 y2 z2 = 1 gives z in terms of x and y implicitly For each x, y, one can solve for the value(s) of z where it holds sin(xyz) = x 2y 3z cannot be solved explicitly for z Prof Tesler 31 Iterated Partial Derivatives Math C / Fall 18 14 / 19 Okay, so you know how to find the derivative of a single variable function as in Calculus 1 But what about multivariable functions?



Http Mathsci Kaist Ac Kr Dykwak Courses Calfall Veccal Main 14 Pdf



Q Tbn And9gcq9arl5ab K Kkztqdma6czzlslnfprp6ljv7o6a18 5qqda4yy Usqp Cau
Given below are some of the examples on Partial Derivatives Question 1 Determine the partial derivative of a function f x and f y if fDerivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series \frac{\partial}{\partial x}(1\div \sqrt{x^{2}y^{2}z^{2}}) en Related Symbolab blog posts Practice, practice, practice Math can be an intimidatingThe ratio of the z component to the x component is the slope of the tangent line, precisely what we know how to compute The slope of the tangent line is fx(a, b), so fx(a, b) = w u = w 1 = w In other words, a vector parallel to this tangent line is 1, 0, fx(a, b) , as shown in figure 1634




Partial Derivative Math Help Forum




Find All The First Order Partial Derivatives For The Chegg Com
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!1 Topic 7 Self Assessment I Partial Differentiation 1 Find all first and second order partial derivatives of the following functions (i) y =x2 2xz z2 x z x y =2 2 ∂ ∂ 2 2 2 = ∂ ∂ x y 2 2 = ∂ ∂ ∂ x z y x z z y =2 2 ∂ ∂ 2 2 2 = ∂ ∂ z y 2 2 = ∂∂ ∂ z x y (ii) y4 Partial Derivatives Recall that for a function f(x) of a single variable the derivative of f at x= a f0(a) = lim h!0 f(a h) f(a) h is the instantaneous rate of change of fat a, and is equal to the slope



13 7 Extreme Values And Saddle Points Mathematics Libretexts




Partial Derivatives Calculus 3
1050 Chapter 14 Partial Derivatives y z x 0 (1, 0, 0) P (0, 0, 1) z x2, y 0 z 2 x2 y Circle x2 y2 1 in the plane z 1 (1, 0, 1) FIGURE 1458 If P is constrained to lie on the paraboloid the value of the partial derivative of with respect to x at P depends on the direction of motion (Example 1) (1) As x changes, with P moves up or down theApproximate partial derivatives from a table If the average value of f on the interval 2 to 4 is 3, then find the integral shown Find the partial derivatives of f (x,y,z)=xyz Find the partial derivatives of f (x,y,z)=xyz Find and interpret the partial derivatives of f (x,y)=3x2y4 1 Answer1 Active Oldest Votes 1 It is correct To justify your feeling, you can apply the chain rule to the maps g x ↦ x 2 y 2 (where y is fixed) and f




1 9 3 We Would Like To Make The Length 6 The Only Vectors In The Same Direction As V Are Those Pdf Free Download



Www Ualberta Ca Rjia Math214 Hwks Sol8 Pdf
Partial Derivative Formulas and Identities There are some identities for partial derivatives as per the definition of the function 1 If u = f (x,y) and both x and y are differentiable of t ie x = g (t) and y = h (t), then the term differentiation becomes total differentiation 2F(x,y)=ln(x^2y^2) 2arctan(y/x) * F=x^2y^2 → dF= 2xdx2ydy * * d(ln(x^2y^2))=d(ln(F)) * = (1/F) dF * * = (1/(x^2y^2))( 2xdx2ydy) * z=y/x → xz=y → zdxxdzExercise 1(a) To calculate the partial derivative ∂z ∂x of the function z = x2y4, the factor y4 is treated as a constant ∂z ∂x = ∂ ∂x x2y4 = ∂ ∂x x2 ×y4 = 2x(2−1) ×y4 = 2xy4 Similarly, to find the partial derivative ∂z ∂y, the factor x2 is treated as a constant ∂z ∂y =




Partial Derivatives




Math 9 Solutions To Assignment 7 X 2y 1 X 2y I 2 F X Cos Y Z F Y X Z Sin Y Z F Z Xy Z 2 Sin Y Z Pdf Free Download
Solve for x x^2/ (u^2 a^2) y^2/ (u^2 a^2) z^2/ (u^2 a^2) = 1 Subtract y^2/ (u^2 a^2) z^2/ (u^2 a^2) from both sides x^2/ (u^2 a^2) = (y^2/ (u^2 a^2) z^2/ (u^2 a^2)) 1 Multiply both sides by u^2 a^2 x^2 = a^2 u^2 y^2 z^2Textbook solution for Calculus Early Transcendentals 8th Edition James Stewart Chapter 143 Problem 43E We have stepbystep solutions for your textbooks written by Bartleby experts!1,x 2)=0 where the partial derivatives are ∂F/∂x 1 = F x 1, ∂F/∂x 2 = F x 2 and ∂F/∂y = F yThis class of functions are known as implicit functions where F(y,x 1,x 2)=0implicity define y = y(x 1,x 2) What this means is that it is possible (theoretically) to rewrite to get y isolated and expressed as a function of x 1 and x 2



Jntua Ac In Gate Online Classes Registration Downloads Material A Pdf




Maxima And Minima



Www Whitman Edu Mathematics Multivariable Multivariable 14 Partial Differentiation Pdf




Lecture Pdf Partial Differential Equation Tension Physics




16 Solved Questions Midterm Exam 2 Vector Calculus Math 223 Docsity



Www Math Ucla Edu Josephbreen Minimization Maximization And Lagrange Multiplier Problems Pdf
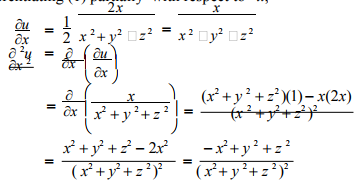



Partial Derivatives Differentiation Business Mathematics Statistics B Com Notes Edurev



Www Ucl Ac Uk Ucahjva Multi4 Pdf




F X Y Z X 2y Y 2z Xz 2 Partial Differential Chegg Com




Partial Derivative Examples Math Insight




Calc 501 1000 By James Bardo Issuu




Doc Chapter Four Derivatives Of Multivariate Functions Partial Differentiation Habtamu Destaw Academia Edu




Partial Derivative Of F X Y Z With Respect To Z Mathematics Stack Exchange




1 Pages 1 33 Flip Pdf Download Fliphtml5




Finding Partial Derviatives Youtube




The Equation 3y Z 3 3xz Defines Z Implicitly As A Function Of X And Y Evaluate All Three Second Partial Derivatives Of Z With Respect To X And Or Y Verify That Z Is A




1 Given F X Y Z As Z 2 Y Find A The Partial Derivative F X Y Homeworklib




Finding Partial Derivatives Implicitly In Exercises Chegg Com
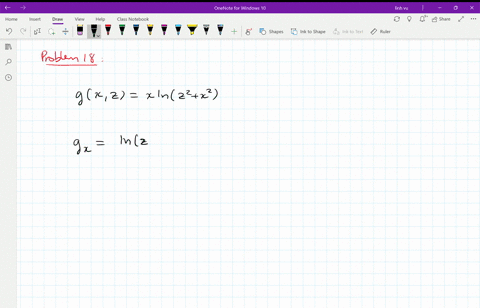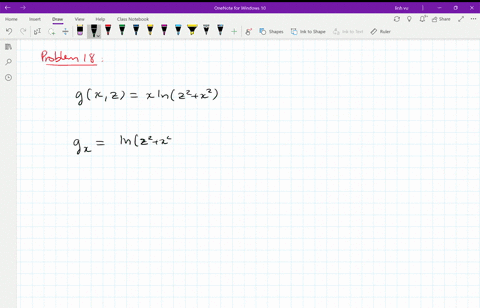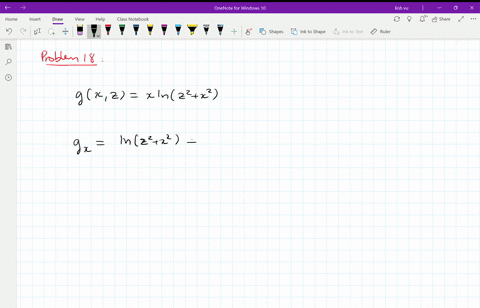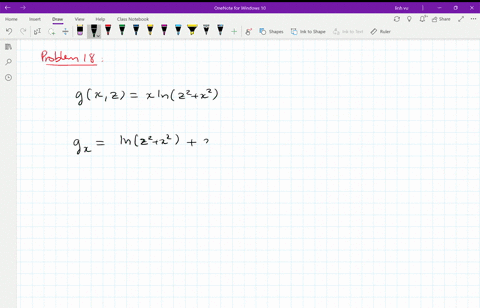



Solved Find The First Partial Derivatives Of The



1




The Partial Derivative Partial Differential Y Partial Chegg Com




14 Partial Derivatives Copyright Cengage Learning All Rights




Partial Differential Equations




If Y 1 Sqrt A 2 X 2 Find Dy Dx




Consider The Function F X Y Ln X 2 Y 2 3 Compute The Partial Derivatives Of The First And Second Order Mathematics Stack Exchange




Contour Integration Wikipedia




Problems On Partial Differentiation U Log X 2 Y 2 Z 2 U Tan 1 2xy X 2 Y 2 Z F X Ay Q X Ay Youtube




Answered 7 Find The Second Partial Derivatives Bartleby
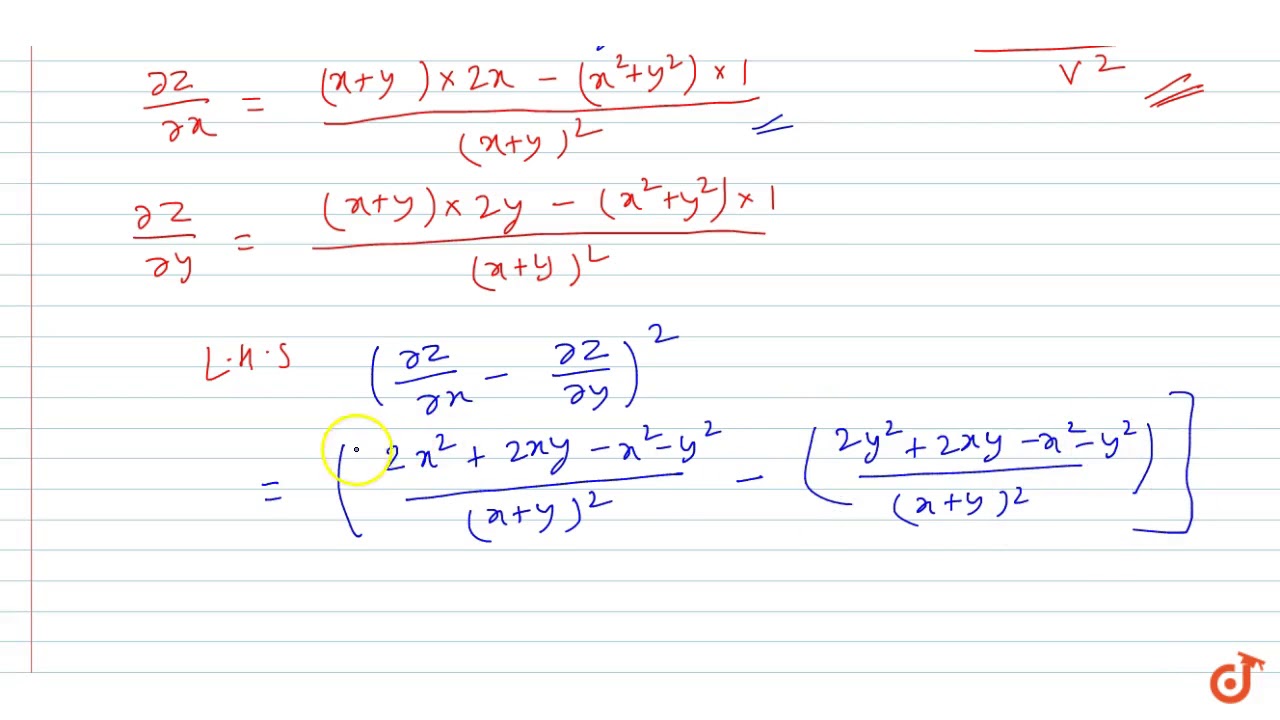



If Z X Y X 2 Y 2 Show That Delz Delx Delz Dely 2 4 1 Delz Delx Del Youtube



If U Log X 2 Y 2 Xy Then X U X Y U Y Is A 0 B U C 2u Sarthaks Econnect Largest Online Education Community
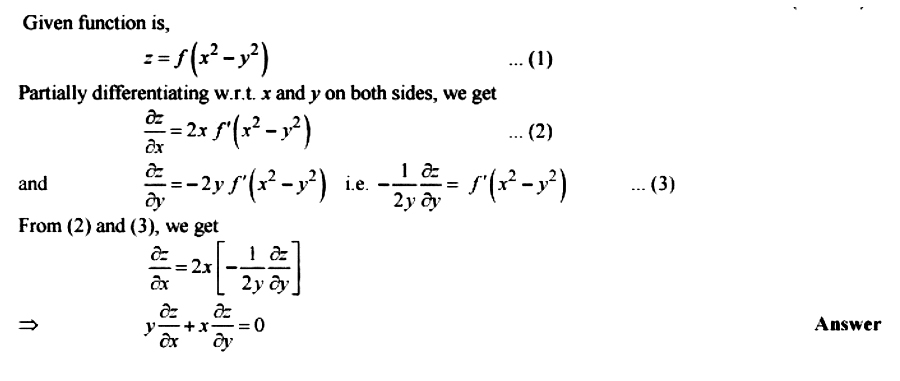



Form A Partial Differential Equation By Eliminating Arbitrary Function From Z F X 2 Y 2 Mathematics 2 Question Answer Collection




Se13e01 01 Gif
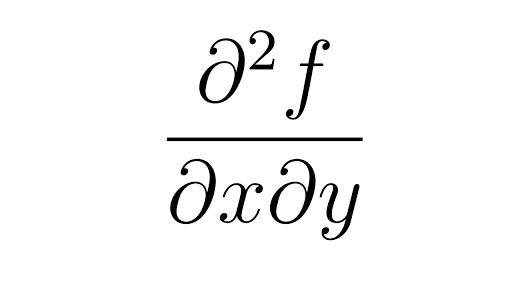



Second Partial Derivatives Article Khan Academy
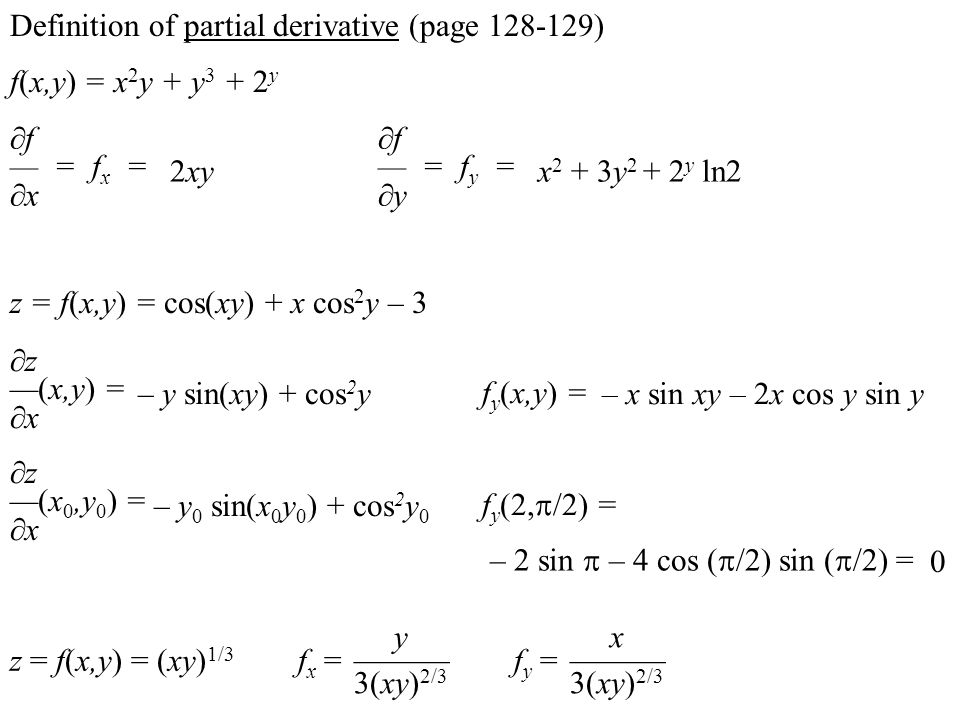



F X Y X 2 Y Y Y F F X X 2xyx 2 3y Y Ln2 Z F X Y Cos Xy X Cos 2




Copyright C Cengage Learning All Rights Reserved Partial Derivatives Ppt Download



1



If U 2 1 X 2 Y 2 Z 2 Then Show That 2u X 2 2u Y 2 2u Z 2 0 Sarthaks Econnect Largest Online Education Community




Partial Derivatives Calculus 3




Partial Differentiation



What Is The Partial Derivative Of U Y X W R T To X And Y Quora




Q7 Find The Second Order Partial Derivative 1 8 U Chegg Com




Chapter 5 Partial Differentiation



Rules Of Calculus Multivariate




Partial Differentiation If Z X Y X 2 Y 2 Show That әz әx әz әy 2 4 1 әz әx әz әy Youtube




Calculus 3 Partial Derivative 14 Of 30 Find More Partial Derivatives Example 2 Of 2 Youtube
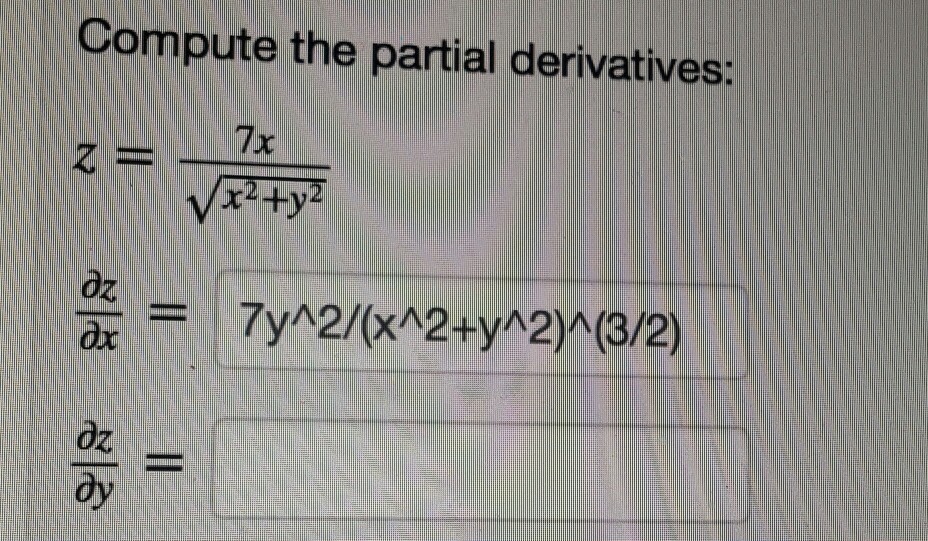



Compute The Partial Derivatives Z 7x Square Root Chegg Com




Compute The Partial Derivatives Z 3x Squareroot Chegg Com




Se Cse Pde Pages 1 17 Flip Pdf Download Fliphtml5




Ma2e01 Tutorial Solutions 3 1 2 Z




Partial Derivative Ln X 2 Y 2
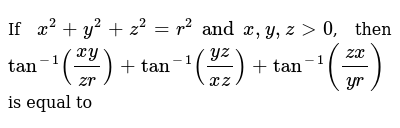



If X 2 Y 2 Z 2 R 2 And X Y Z 0 Then Tan 1 Xy Z
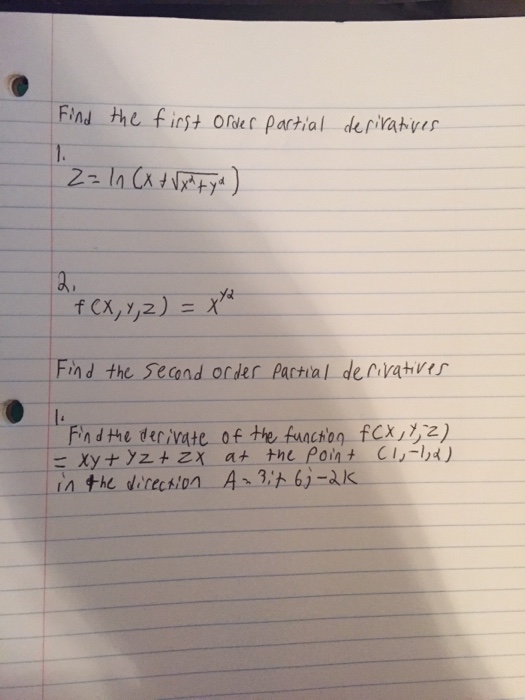



Find The First Order Partial Derivatives Z Ln X Chegg Com




Partial Differentiation




Partial Derivatives Practice Studocu




Implicit Differentiation Advanced Example Video Khan Academy




Find The Indicated Partial Derivatives Math F W X Y Z Sqrt X Y Y Z X 3 Sin Sqrt W 2 Z 2 F X X F Y Y F W X Y Z Math Homework Help And Answers Slader



Http Core Csu Edu Cn Nr Rdonlyres Mathematics 18 02spring 06 0a8acd95 46d6 44 8d79 C7ca6630cd8b 0 Part Diff Sol Pdf




F X Y Cos Xy 2 A Partial Differential 2 Chegg Com



Http Www Pstat Ucsb Edu Faculty Hohn 2110q S15 Worksheets Worksheet 3 Sol Pdf



Derivative Calculator With Steps



How To Eliminate The Arbitrary Function And Hence Obtain The Partial Differential Equation Z X Y F X 2 Y 2 Quora




If U Log X 2 Y 2 Z 2 Verify 2u X Y 2u X Y
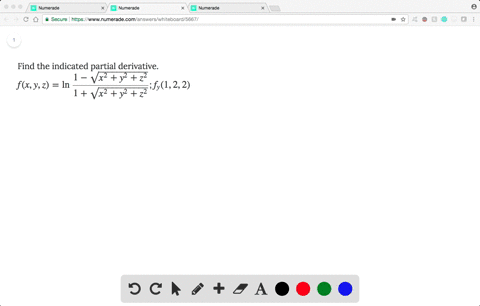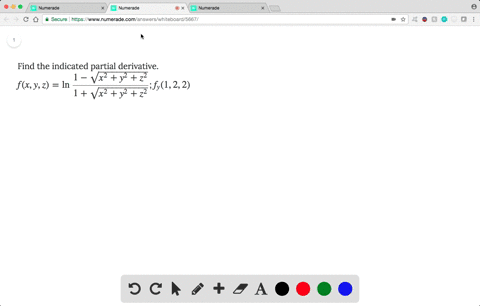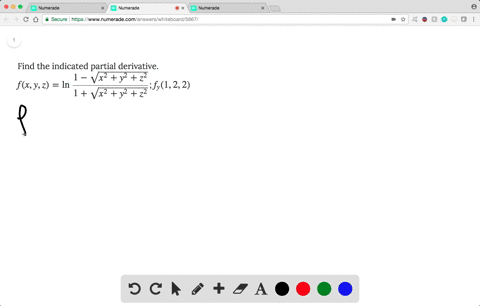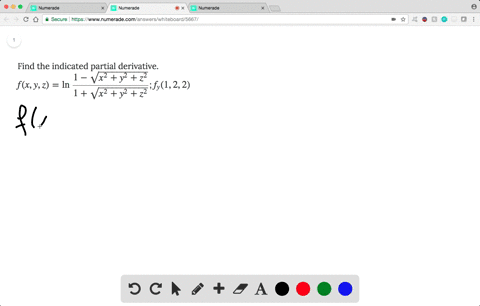



Solved Find The Indicated Partial Derivative F X



Partial Derivatives Boundless Calculus



Solved Find All The First And Second Order Partial Derivatives Of F X Y X 2y 2 E Xy Sin X 2y Course Hero




Contour Integration Wikipedia



Solved Determine The Second Partial Derivatives Of F X Y Z Tan 5 2x2y4z2 Xx 4y42 8x2y422tan 2x2y422 5 1 Sec 2x2y4 2 5 Course Hero




14 Partial Derivatives Copyright Cengage Learning All Rights




Homework 14 5




Practice Problems 10 And 11




Level Surfaces



Users Math Msu Edu Users Gnagy Teaching 11 Fall Mth234 Mth234 061 E2 F10 Pdf




How To Take The Derivative Of This Function Mathematics Stack Exchange



Search Q Derivative Of Ln 2x Tbm Isch



Http Www Mit Edu Hlb 1802 Notes Apm Jmo Pdf Mit18 02sc Supprobsol2 Pdf




Partial Derivatives Archives Www Tinspireapps Com Blog



0 件のコメント:
コメントを投稿